配分函数的理解
配分函数的由来
从玻尔兹曼统计可得 $$ N_i = N \frac{g_i e^{-\varepsilon_i/kT}}{\sum_i g_i e^{-\varepsilon_i/kT}} $$ 即 $$ \frac{N_i}{N} = \frac{g_i e^{-\varepsilon_i/kT}}{\sum_i g_i e^{-\varepsilon_i/kT}} $$ 其中$N_i$代表能级$\varepsilon_i$上分布的粒子数目,$N$是总粒子数目。$g_i$是能级简并度,$k$是玻尔兹曼常数,$T$是温度。
由此可得,在平衡分布(最概然分布)下,在第$i$个能级上的粒子数目与总粒子数目之比满足上述关系式。因为左边的式子反映了粒子在各可能的能级上的分配特性,为了方便表示,将分母用$q$来代替表示,命名为配分函数。
$$ \begin{align} \frac{N_i}{N} &= \frac{g_i e^{-\varepsilon_i/kT}}{\color{red}{\sum_i g_i e^{-\varepsilon_i/kT}}} \\ \frac{N_i}{N} &= \frac{g_i e^{-\varepsilon_i/kT}}{\color{red}{q}} \end{align} $$
配分函数的讨论
从配分函数的形式,可以从数学变换的角度去理解。
我们观察一下配分函数的表达式 $$ q = \sum_i \color{red}{g_i e^{-\varepsilon_i/kT}} $$ 配分函数是个求和的式子,不妨观察一下求和的部分,为了方便描述,我们将这部分表达式命名为玻尔兹曼因子 $$ f = g_i e^{-\varepsilon_i/kT} $$ 由此,我们即可将配分函数概括为玻尔兹曼因子之和。那么,玻尔兹曼因子又如何去理解呢?
在物理学中,玻尔兹曼因子是一个权重因子,它决定了在温度$T$时处于热力学平衡的多状态系统中状态$i$的相对概率。
而在解析几何中,常见的数学变换可粗略地分为线性变换和非线性变换。我们可以思考一种非线性变换-指数变换,其输入输出满足以下形式 $$ f(x) = a \cdot e^{bx} $$ 又因为通常参数$b$是负数,也可称其为负指数变换。
通过对比,可以将玻尔兹曼因子在数学变换的角度上理解为能级$\varepsilon_i$的指数变换 $$ f(\varepsilon_i) = a \cdot e^{b\varepsilon_i} $$ 其中 $$ \begin{cases} a = g_i \\ b = -\frac{1}{kT} \end{cases} $$
负指数函数的讨论 $$ y = e^{-x/t} $$
该函数的值域在$(0,1]$,是单调递减函数。当参数$t$越小时,函数的图像分布越窄。
不难发现,在平衡分布下某个能级上的粒子数目比值与其玻尔兹曼因子成正比 $$ \begin{align} \frac{N_i}{N} &= \frac{g_i e^{-\varepsilon_i/kT}}{\sum_i g_i e^{-\varepsilon_i/kT}} \\ \frac{N_i}{N_j} &= \frac{g_i e^{-\varepsilon_i/kT}}{g_j e^{-\varepsilon_j/kT}} \end{align} $$ 由负指数函数的性质可知,在越高的能级上粒子数目越少,在越低的能级上粒子数目越多(负指数函数的单调性)。而当温度$T$越低时,粒子整体处于较低能级的概率越高。当温度$T$无限接近于绝对零度时,所有粒子都将处于能量最低的基态。
指数变换的联想
虽然我们可以将玻尔兹曼因子认为是一种数学变换-指数变化,但事实真正大量使用解析几何数学变换的地方并非是物理化学或统计热力学,而是计算机图形学。
在计算机中图片(位图)是通过像素点矩阵保存的,通过对这个像素点矩阵做各种数学变换可以得到不同种图片过滤后的结果。
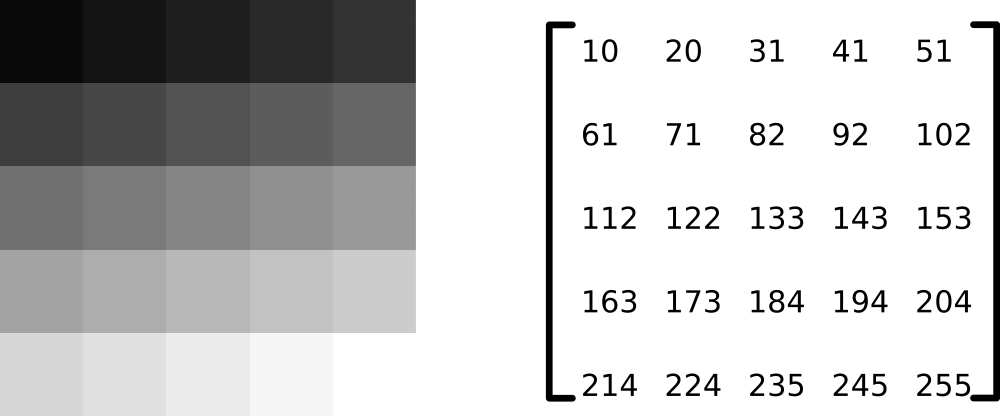
如对以下灰度图进行指数变化

可以类比玻尔兹曼分布。接近白色的像素点值高,而接近黑色的像素点值低。将左边的原图视为能级的二维分布图,而右边变换后的图像视为粒子数目分布图。可以发现,左边接近白色的地方(高能级)在右边切变成了接近黑色(粒子数目少)。
Softmax函数
在数学,尤其是概率论以及机器学习相关领域中,Softmax函数,或称归一化指数函数。其表达式通常为: $$ \sigma(x_i) = \frac{e^{x_i}}{\sum_i e^{x_i}} $$ 看这个形式是否与玻尔兹曼分布公式十分类似。玻尔兹曼分布公式和softmax函数有一定的关联,事实上softmax函数是玻尔兹曼分布公式的一种推广应用。
玻尔兹曼分布是一种描述粒子分布的概率分布函数,通常用于描述系统在热平衡状态下的分布情况。而softmax函数则是将一个向量映射到[0,1]之间的概率分布函数,它可以用来将一个向量中的元素转化为概率分布。二者的关联在于它们都是利用指数函数来进行概率分布的建模。历史上,softmax函数的提出者们在提出它的时候,可能参考了玻尔兹曼统计中的思想和方法,尤其是玻尔兹曼的概率分布思想。他们是受到了玻尔兹曼分布的启发,将其推广到了神经网络中。
从中也可看出,人工智能的底层技术受到了多学科交叉的影响。而掌握基础的自然科学有助于更好地去理解与扩展人工智能算法的研究。
这或许是一种跨学科思维的概念对比,也可能是个不恰当的比喻。欢迎大家给出更多关于配分函数的思考与理解方式。