关于水-乙醇体系偏摩尔体积引发的一系列思考与探究实践这件事

事件背景

乌拉同学最近在MATLAB软件学习上遇到了困惑，虽然在过去两年他学习了7门编程语言，写了5万行有效代码，每周还有两门MATLAB相关的工程数学建模与人工智能数学课程，但在学习MATLAB上进度无比缓慢，仿佛一直都在起跑线。他甚至水了两次数模MATLAB作业（主要是那糟糕线性代数基础），为此他心里一直很愧疚:pensive: 他觉得主要原因是缺乏学习动力，找不到合适的MATLAB软件应用场景。

MATLAB是美国MathWorks公司出品的商业数学软件，用于数据分析、无线通信、深度学习、图像处理与计算机视觉、信号处理、量化金融与风险管理、机器人，控制系统等领域。 MATLAB是matrix&laboratory两个词的组合，意为矩阵工厂（矩阵实验室），软件主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中，为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案，并在很大程度上摆脱了传统非交互式程序设计语言（如C、Fortran）的编辑模式。 MATLAB与一般的编程语言大不一样，它在面向数学与科研的编程功能远超C、Python等通用编程语言，可以做很多偏底层语言做不了的事情（从图灵完备性的角度来看，也不是真的做不了，除非从零开始造轮子）。

事件经过

==50mL水和50mL乙醇混合后是100mL的溶液吗？==

依据以往的知识，我们知道答案比100mL小。

混合后的体积具体是多少我们可以使用直接去做实验，那还有其他办法吗？

在物理化学课上乌拉同学学习了偏摩尔体积的概念。虽然前一天晚上他也预习了这一知识点，但是却没发现其中的奥秘。在老师提到偏摩尔体积就是混合体系体积对某一组态的摩尔数的偏导数，并联系到极限思想时，乌拉同学恍然大悟。

恍然大悟1

偏摩尔量

对于一个仅做体积功的$K$组分均匀体系，其任一广度性质$Z$可表示为函数：

$$ Z = Z(T,p,n_1,n_2,…,n_i,…,n_K) $$

若体系状态发生了微小变化，$Z$的全微分为：

$$ \mathrm d Z = \left ( \frac{\partial Z}{\partial T} \right)_{p,n} \mathrm d T + \left( \frac{\partial Z}{\partial p} \right)_{T,p} \mathrm d p + \sum_{i=1}^K \left( \frac{\partial Z}{\partial n_i} \right)_{T,p,n_j} \mathrm d n_i $$

下标$n$表示所有组分的物质的量都不变；$n_j$ 表示除$n_i$外其余组分的物质的量不变。

广度性质$Z$的偏摩尔量被定义为：

$$ Z_i = \left( \frac{\partial Z}{\partial n_i} \right)_{T,p,n_j} $$

称为$i$组分的偏摩尔$Z$.

则$i$组分的偏摩尔体积为： $$ V_i = \left ( \frac{\partial V}{\partial n_i} \right)_{T,p,n_j} $$ 等温、等压、组成不变时，单位物质的量的$i$在确定组成的混合物中对体积的贡献$V_i$称为物质$i$的偏摩尔体积。由此可得，当温度、压强、组成确定时，偏摩尔体积也是确定的。

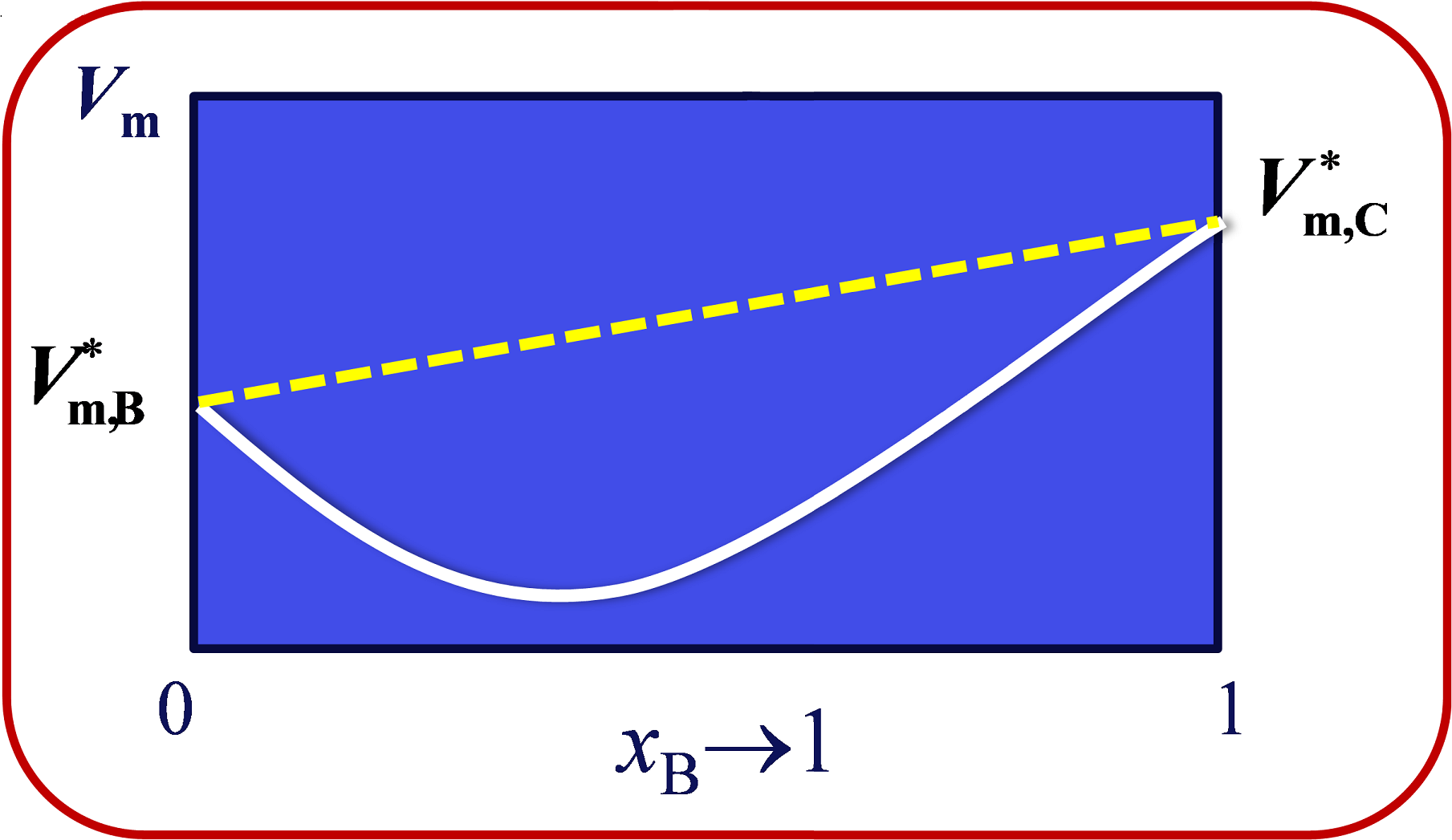
恍然大悟2

统计学的贡献

统计学的力量远远大于常人对他的理解，事实上人类科学史上80%以上的科学规律都是通过统计学方法总结而来的。而化学这门学科有诸多经验性知识总结，这些经验性知识从何而来，历史上化学家们是如何认知客观世界，并得到我们今天所学的知识的，值得我们思考。

恍然大悟3

数学模型是利用系统化的符号和数学表达式对问题的一种抽象描述。数学建模可看作是把问题定义转换为数学模型的过程。 数学建模是数学与世界其他地方（其他领域）之间建立的联系的方法。(《Mathematical Modeling》教材定义)

数学建模一般流程

数学建模一般流程

研究目的及意义

设计定量实验测量不同水-乙醇摩尔比下的混合体系的体积。
使用混合体系的体积的散点数据进行非线性拟合得到偏摩尔体积曲线。
这个探究需要数学建模，而MATLAB正是非常出色的数学建模软件，在学习物理化学的同时还能加强MATLAB建模，一举两得。
进行跨学科探究实践，加强数学建模能力与科学思维能力。

这期间乌拉同学把测量偏摩尔体积的想法分享给了一些周边的同学，他从余正阳同学那里得到两个建设性意见：

把求解偏摩尔体积的过程类比于范德华方程的求解过程。
测量混合物组态的体积方法使用比重瓶来实现。

范德华方程是对理想气体状态方程的一种改进，特点在于将被理想气体模型所忽略的的气体分子自身大小和分子之间的相互作用力考虑进来，以便更好地描述气体的宏观物理性质。

$$ \left(p+\frac{a^{\prime}}{v^{2}}\right)\left(v-b^{\prime}\right)=k T $$

事实上，范德华方程就是通过数学建模的方法得到的经验公式。**使用数学建模得到的结果原则上都是近似解，答案不唯一。**也就是人们也可以用其他模型来描述实际气体的状态。

在测量体积方面乌拉同学只想到了直接使用量筒的方法，而余正阳同学建议的比重瓶可以更加准确测量混合液体体积。在经过查阅资料后乌拉同学也觉得这个实验应该使用比重瓶测量体积，因为液体的质量可以使用电子天平准确测量，只要知道密度就可计算出体积。但是时间成本有限，乌拉同学未能掌握使用比重瓶测量偏摩尔体积的具体实验步骤，另外实验室的负责老师也表示借用比重瓶可能要等等。所以最终实验方案还是使用量筒来测定体积。

实验探究

实验目的

记录恒定的温度与压强情况下不同体积比的蒸馏水与乙醇混合后的体积。
通过不同摩尔比的混合溶液体积散点数据进行非线性曲线拟合。
提高自主跨学科探索实践能力与知识认知的独立思考能力。

实验仪器与试剂

3个50mL量筒、10mL移液枪。

纯乙醇，蒸馏水。

实验步骤

取出1个50mL量筒，加入15mL纯乙醇。
量筒中加入1mL、3mL、5mL、10mL、15mL、20mL、25mL、30mL、35mL蒸馏水，并记录混合后的总体积。
再取出1个50mL量筒，加入15mL蒸馏水。
量筒中加入1mL、3mL、5mL、10mL、15mL、20mL、25mL、30mL、35mL纯乙醇，并记录混合后的总体积。
导入数据数据至MATLAB软件，进行数据处理。
使用MATLAB软件对该散点数据进行非线性曲线拟合，得到回归曲线。（也可以考虑更复杂的数学模型或者机器学习模型）
对该曲线进行求导，得到恒定的温度与压强情况下水-乙醇体系偏摩尔体积预测曲线，并绘图。

温度：22.3℃

压强：101.325kPa

V_H₂O/mL	V_C₂H₅OH/mL	V_总/mL
1	15	15.8
3	15	17.7
5	15	19.5
10	15	24.2
15	15	29.1
20	15	34.0
25	15	39.0
30	15	44.0
35	15	49.0
15	1	16.0
15	3	18.0
15	5	19.9
15	10	24.3
15	15	29.1
15	20	34.0
15	25	38.8
15	30	43.8
15	35	48.7

从数据记录来看，在恒温恒压条件下，相同的摩尔比的水的偏摩尔体积要大于乙醇的偏摩尔体积。也就是混合体系中的水的体积贡献要大于乙醇的体积贡献。

数学建模

这类使用散点数据进行非线性拟合属于回归预测类问题。乌拉同学将分别使用凸函数模型进行回归处理。由于寻找偏摩尔体积的目的是为了知道在恒温恒压下确定的摩尔比增加单位体积时对总体积的贡献是多少，所以将回归预测的输入变量设为水的体积比，准确的来说是体积百分比（体积分数），摩尔比确定的同时体积比也是确定的，实际情况下体积比可能用的更多。将单位体积的增量作为回归预测的输出变量。

数学模型非线性拟合

由乌拉同学的先验知识可知，体积增量贡献与体积比的关系近似为耐克函数。所以将使用类耐克函数进行非线性拟合。

对勾函数（耐克函数）是一种类似于反比例函数的一般双曲函数，是形如f(x)=ax+b/x（ab＞0）的函数。由图像得名，又被称为“双勾函数”“勾函数”“对号函数”“双飞燕函数”等。常见a=b=1。

乌拉同学想出的函数模型长这样： $$ y = ax + \frac{c}{bx} + d $$ 求解这个非线性函数模型的拟合参数是一个数学优化问题，这里会用到一些迭代算法，如矩阵表示的最小二乘法。而乌拉同学其实学的也不深，但是MATLAB软件有现成的工具包可以直接做非线性拟合。

输入至MATLAB软件进行求解该方程参数

1
2
3
4
5
6
7
8


% 函数脚本
function y = func(beta,X)
    a = beta(1);
    b = beta(2);
    c = beta(3);
    d = beta(4);
    y = a*X + c./(b*X) + d;
end

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


clear;clc
H2O = [1 3 5 10 15 20 25 30 35 15 15 15 15 15 15 15 15 15];
C2H5OH = [15 15 15 15 15 15 15 15 15 1 3 5 10 15 20 25 30 35];
x0 = H2O./(H2O+C2H5OH);
V = [15.8 17.7 19.5 24.2 29.1 34 39 44 49 16 18 19.9 24.3 29.1 34 38.9 43.8 48.7];
y0 = V./(H2O+C2H5OH);
beta0 = [1 1 1 1];
[p] = lsqcurvefit(@func,beta0,x0,y0);	% 非线性拟合
xp = 0.05:0.01:1;
yp = func(p,xp);
figure;
plot(x0,y0,'ko');
hold on;
plot(xp,yp);
grid on;

回归的得到参数分别为： $$ \begin{cases} a = 0.0477 \\ b = -648.9982 \\ c = -1.7081 \\ d = 0.9468 \end{cases} $$ 函数模型为： $$ y = 0.0477x + \frac{1.7081}{648.9982x} + 0.9468 $$ 从图中可以看出，偏摩尔体积的极值大致在体积分数为0.2的位置。而查相关文献的参考数据的话体积分数应该在0.05附近取偏摩尔体积的极值。这也是为什么我们常用95%乙醇。所以乌拉同学的模型效果可能并不理想，问题主要还是出在了没有办法精确测量混合体系的体积。

回顾反思

在实验过程中会发现系统误差其实是很大的，等体积的水和乙醇混合之后虽然不是原体积的两倍，但是变化其实很少。如图所示，在读取量筒体积测量值时就可能产生不小的人为误差，而我们要捕获的差异值也就1mL左右，产生的误差也差不多。那样的话，这种定量实验本身也就没太大意义了。这种微小的变化的测量就需要新的测量方法或者仪器，这里就可以考虑余正阳同学建议比重瓶法，但是依旧可能面临其他系统误差。

总体而言该探究方式虽然是为了定量分析，但是太粗糙了，得到的模型结果也只能用于定性判断。对于乌拉同学来说，非常重视以自身优势领域为中心向其他领域四周扩散，活学活用的理念。所以探究过程的意义大于探究结果的本身。之后也会在学习与生活中发现各种可探究、有收获的原创实践，也欢迎大家一起交流学习。