数学建模

元启发式算法-模拟退火算法MATLAB实现

模拟退火求解函数最大值

模拟退火介绍

模拟退火算法来源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。这是一种经典的元启发式算法模型，可用于组合优化等问题。

Metropolis准则

若在温度$T$，当前状态$i$ → 新状态$j$

若$E_j<E_i$，则接受$ j $为当前状态；

否则，若概率 $p=e^{[-(E_j-E_i)/KT]}$ 大于$[0,1)$区间的随机数，则仍接受状态$ j $为当前状态；若不成立，则保留状态$ i $为当前状态。

$p=e^{[-(E_j-E_i)/KT]}$：在高温下，可接受与当前状态能量差较大的新状态；在低温下，只接受与当前状态能量差较小的新状态。

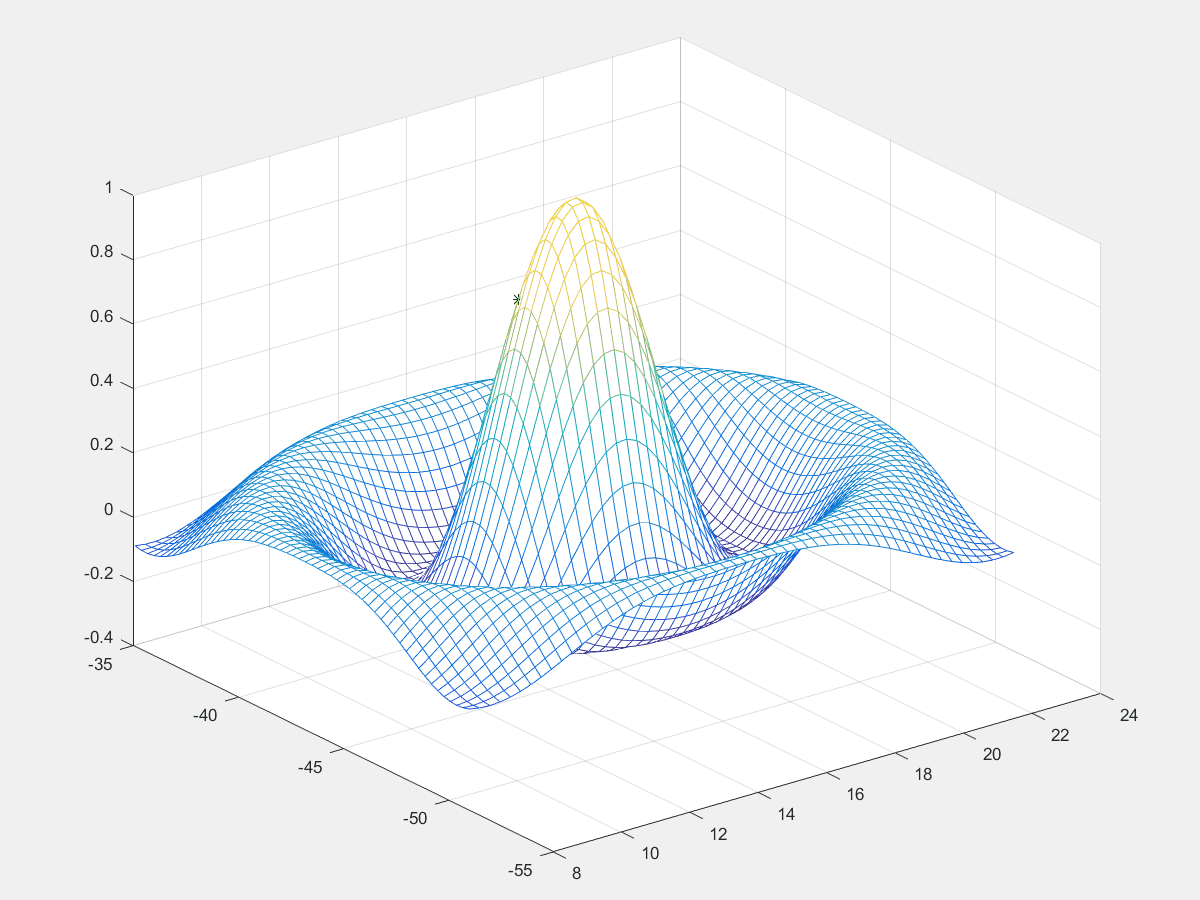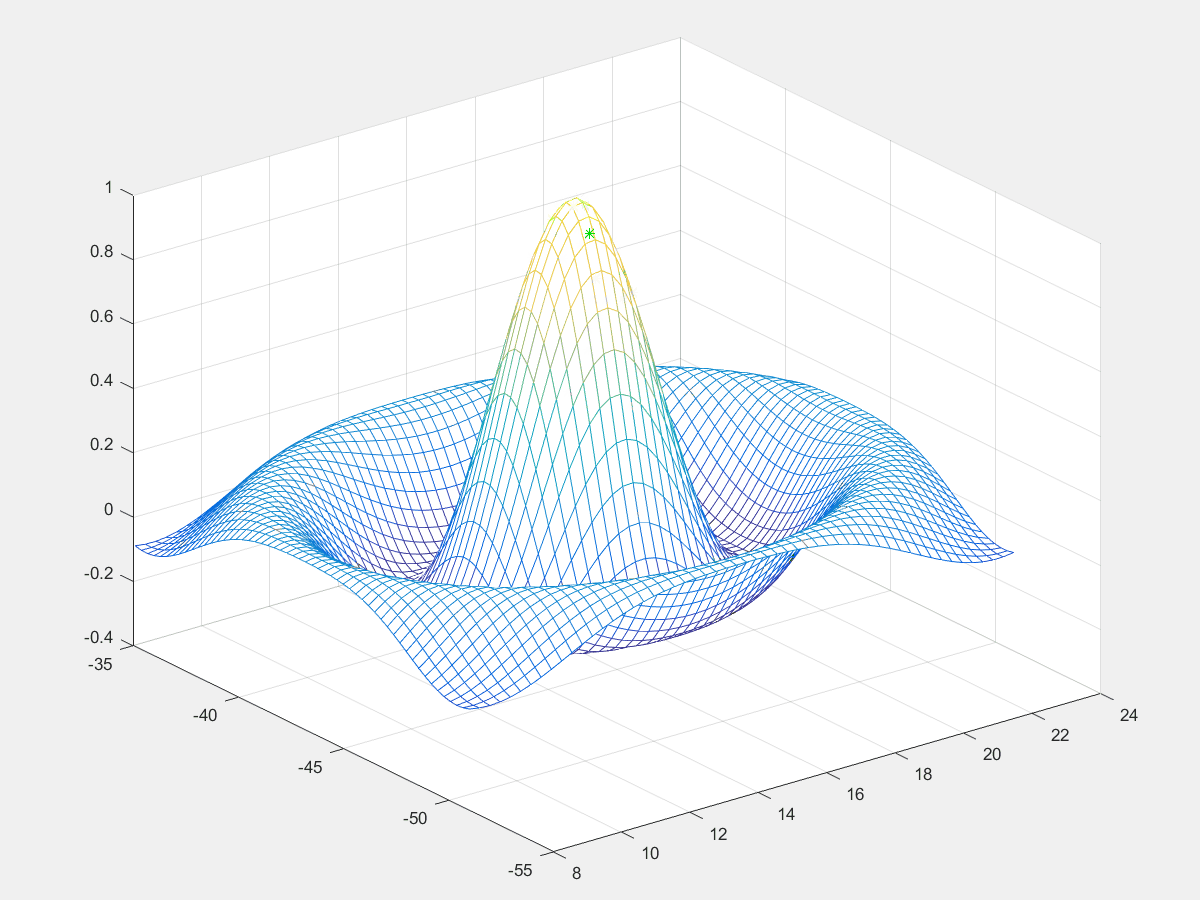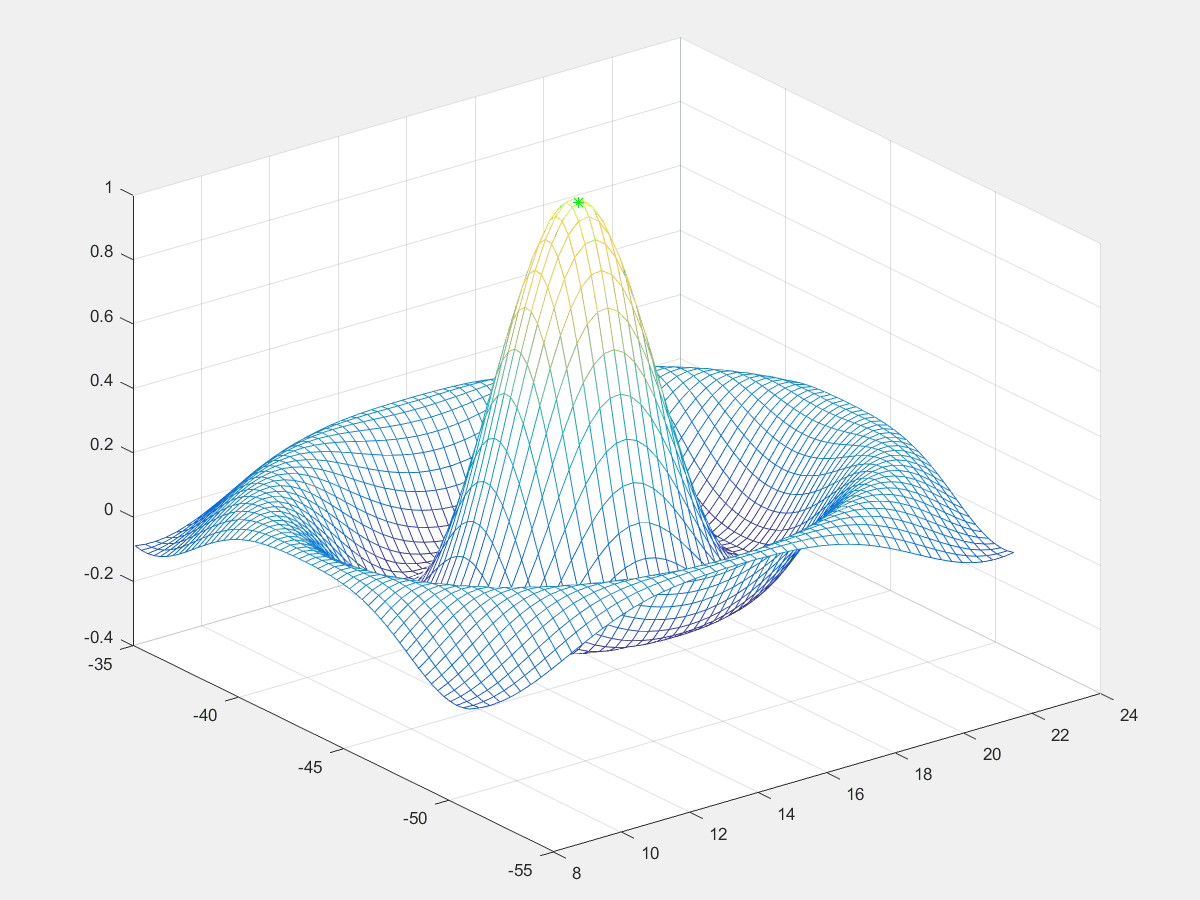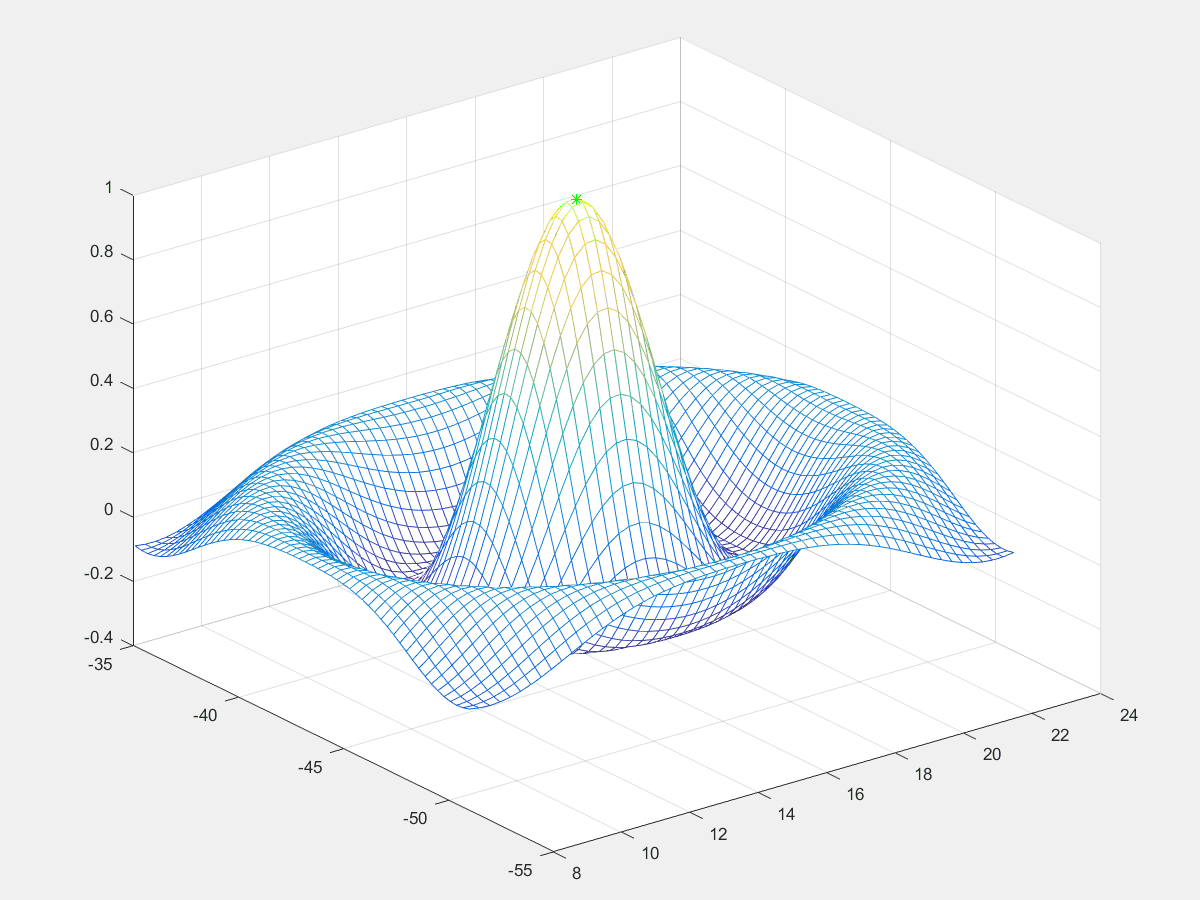
寻找函数最大值

寻找以下二元函数的最大值 $$ z(x,y) = \frac{\sin{\left(\sqrt{(x-16)^2+(y+43)^2}\right )}} {\sqrt{(x-16)^2+(y+43)^2}} $$ g

Matlab代码 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

% 目标函数
f = @(x,y) sin(sqrt((x-16).^2 + (y+43).^2))./sqrt((x-16).^2 + (y+43).^2);
% 绘制曲线
t1 = 8:0.3:24;
t2 = -51:0.3:-35;
[T1,T2] = meshgrid(t1,t2);
T3 = f(T1,T2);
figure
set(gcf,'position',[250 100 1000 800])
mesh(T1,T2,T3);
hold on

% 退火参数
T = 2;              % 初始温度
d = 0.995;          % 降温幅度
eps = 1e-5;         % 收敛温度
x_min = 8;          % x搜索下限
x_max = 24;         % x搜索上限
y_min = -51;        % y搜索下限
y_max = -35;        % y搜索上限
dx = x_max-x_min;   % x区间大小
dy = y_max-y_min;   % y区间大小

x = x_min + dx*rand();  % x初始值
y = y_min + dy*rand();  % y初始值
z = f(x,y);

h = plot3(x,y,z,'g*');  % 绘制当前点

while T > eps
    x_ = x + (2*dx*rand()-dx)*T;
    y_ = y + (2*dy*rand()-dy)*T;
    while x_ > x_max || x_ < x_min
        x_ = x + (2*dx*rand()-dx)*T;
    end
    while y_ > y_max || y_ < y_min
        y_ = y + (2*dy*rand()-dy)*T;
    end
    z_ = f(x_,y_);
    if z_ > z
        x = x_;
        y = y_;
        z = z_;
    elseif exp((z_-z)/T) > rand() % Metropolis准则
        x = x_;
        y = y_;
        z = z_;
    end
    % 暂停一下更新点位置
    pause(0.01);
    h.XData = x;
    h.YData = y;
    h.ZData = z;
    % 退火
    T = T*d;
end

disp('x,y,z=');
disp(x);
disp(y);
disp(z);

输出结果

1
2
3
4

x,y,z=
   16.0105
  -43.0445
   0.9997
comments powered by Disqus