旋转公式

$$ \begin{cases} x = x_0 \cos \theta - y_0 \sin \theta \\ y = x_0 \sin \theta + y_0 \cos \theta \end{cases} $$

向量法基底法证明

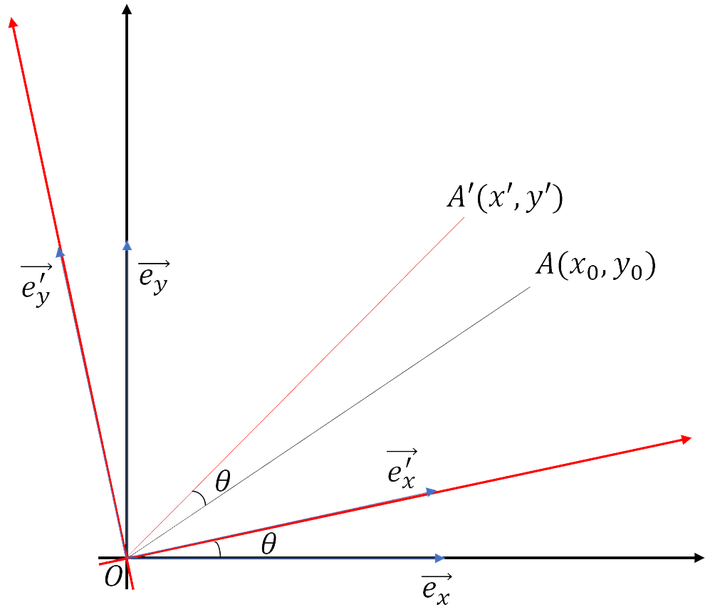
分别用基底向量表示： $$ \begin{cases} \vec{OA} = x \vec e_x + y \vec e_y \\ \vec{OA’} = x \vec e’_x + y \vec e’_y \end{cases} $$ 观察两对基底向量的几何关系可知： $$ \begin{cases} \vec e’_x = \vec e_x \cos \theta + \vec e_y \sin \theta \\ \vec e’_y = -\vec e_x \sin \theta + \vec e_y \cos \theta \end{cases} $$ 进一步推导可得： $$ \begin{align} \vec{OA’} &= x(\vec e_x \cos \theta + \vec e_y \sin \theta) + y(-\vec e_x \sin \theta + \vec e_y \cos \theta) \\ &= (x \cos \theta - y \sin \theta) \vec e_x + (x \sin \theta + y \cos \theta) \vec e_y \end{align} $$ 由此可得： $$ \begin{cases} x’ = x \cos \theta - y \sin \theta \\ y’ = x \sin \theta + y \cos \theta \end{cases} $$

向量表示法证明

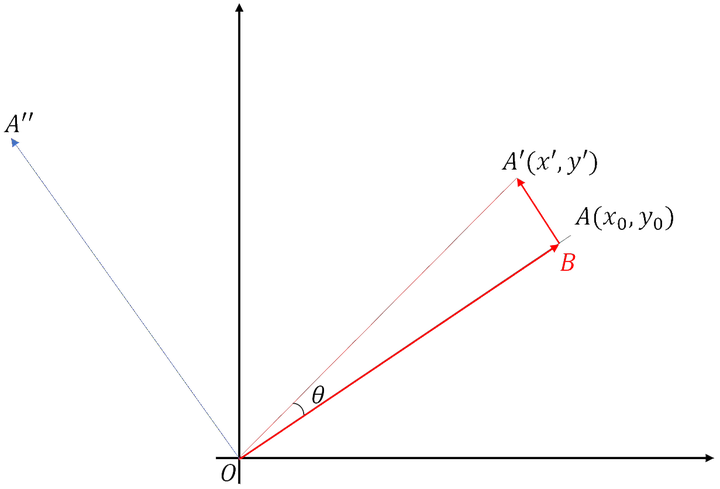
图中的$OA,OA’,OA’’$线段的长度均相等，其中$OA$与$OA’’$相垂直。

由几何关系可知： $$ \vec{OA’} = \vec{OB} + \vec{BA’} $$ 进一步表示： $$ \begin{align} \vec{OA’} &= \vec{OB} + \vec{BA’} \\ &= \frac{|\vec{OB}|}{|\vec{OA}|} \vec{OA} + \frac{|\vec{BA’}|}{|\vec{OA’’}|} \vec{OA’’} \\ &= \frac{|\vec{OB}|}{\color{red}{|\vec{OA’}|}} \vec{OA} + \frac{|\vec{BA’}|}{\color{red}{|\vec{OA’}|}}\vec{OA’’} \\ &= {\color{red}{\cos \theta}} \vec{OA} + {\color{red}{\sin \theta}} \vec{OA’’} \end{align} $$ 由易知$\vec{OA},\vec{OA’},\vec{OA’’}$的向量坐标为：$(x,y),(x’,y’),(-y,x)$ $$ \begin{align} (x’,y’) &= \cos \theta (x,y) + \sin \theta (-y,x) \\ (x’,y’) &= (x \cos \theta -y \sin \theta,x \sin \theta + y \cos \theta) \end{align} $$ 即可得： $$ \begin{cases} x’ = x \cos \theta - y \sin \theta \\ y’ = x \sin \theta + y \cos \theta \end{cases} $$

复数表示法证明

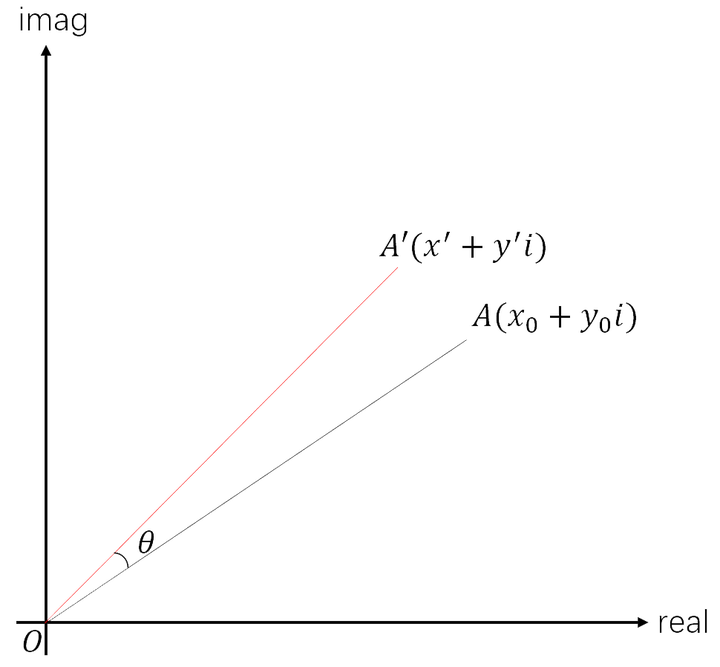
一个复数乘$e^{i \theta}$相当于模不变逆时针方向旋转了$\theta$角。

欧拉公式：$e^{i \theta} = \cos \theta + i \sin \theta$

列出复数关系式并推导： $$ \begin{align} x’ + y’ i &= (x + y i) e^{i \theta} \\ &= (x + y i)(\cos \theta + i \sin \theta) \\ &= (x \cos \theta - y \sin \theta) + (x \sin \theta + y \cos \theta) i \end{align} $$ 实部与实部相等，虚部与虚部相等： $$ \begin{cases} x’ = x \cos \theta - y \sin \theta \\ y’ = x \sin \theta + y \cos \theta \end{cases} $$