一元线性回归与梯度下降

生成数据

生成线性相关的散点数据

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


import numpy as np
import matplotlib.pyplot as plt

num = 20	# 散点数目

# 数据生成
px = np.arange(num)
py = 2*px-4+5*np.random.random(num)	# 加上噪声

# 散点图
plt.scatter(px,py)
plt.show()

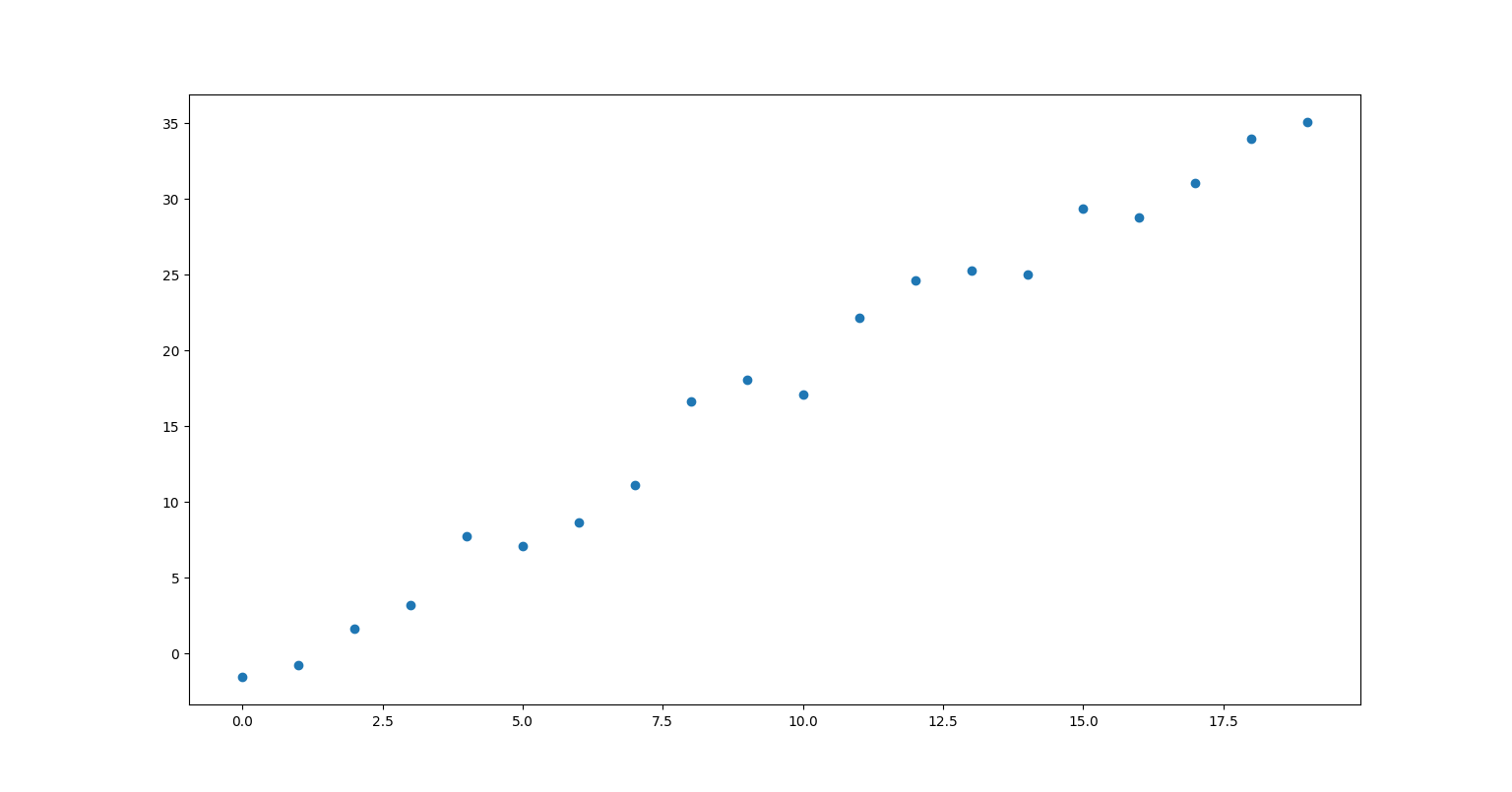
Figure_1

线性回归模型

$$ y = kx + b $$

我们需要找到一个合适的参数k和b模型的预测值与真实值差异最小化。

预测值与真实值差异使用均方误差来体现： $$ L(k,b) = \frac{1}{2n} \sum_{i=1}^{n} (\hat y_i - y_i)^2 = \frac{1}{2n} \sum_{i=1}^{n} (k x_i + b - y_i)^2 $$ 其中$\hat y$是预测值，$y$是真实值。直观的来看，就是所有预测点到真实点的距离平均值的一半。这个式子我们也叫做损失函数。

梯度下降法

为了得到总误差最小的线性模型，我们将使用梯度下降法。

梯度下降法的迭代关系式： $$ \begin{align} k_i &= k_{i-1} - \alpha \cdot \frac{\partial L}{\partial k_{i-1}} \ b_i &= b_{i-1} - \alpha \cdot \frac{\partial L}{\partial b_{i-1}} \end{align} $$ 其中$\alpha$是步长，也称学习率。这里的$k_0,b_0$我们可以随机初始化一个数字。

通过微积分公式我们可以计算得知： $$ \begin{align} \frac{\partial L}{\partial k} &= \frac{1}{n} \sum_{i=1}^{n} (k x_i + b - y_i) \cdot x_i \ \frac{\partial L}{\partial b} &= \frac{1}{n} \sum_{i=1}^{n} (k x_i + b - y_i) \end{align} $$

算法实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44


# 模型函数
def f(x,k,b):
    return k*x+b

# 损失函数
def L(x,y,k,b):
    s = 0
    n = len(x)
    for i in range(len(x)):
        s += (k*x[i]+b-y[i])**2
    return s/2

# k梯度
def grad_k(x,y,k,b):
    s = 0
    n = len(x)
    for i in range(n):
        s += (k*x[i]+b-y[i])*x[i]
    return s/n

# b梯度
def grad_b(x,y,k,b):
    s = 0
    n = len(x)
    for i in range(n):
        s += (k*x[i]+b-y[i])
    return s/n

# 初始化参数
k = 0
b = 0

times = 100		# 训练次数
alpha = 0.01	# 步长

for i in range(times):
    # 梯度下降迭代
    k = k - alpha*grad_k(px,py,k,b)
    b = b - alpha*grad_b(px,py,k,b)
    if i%20 == 0:
        print("%d:%.2f"%(i,L(px,py,k,b)))	# 输出当前损失函数

plt.plot(px,f(px,k,b),c = "red")	# 绘制训练结果
plt.show()

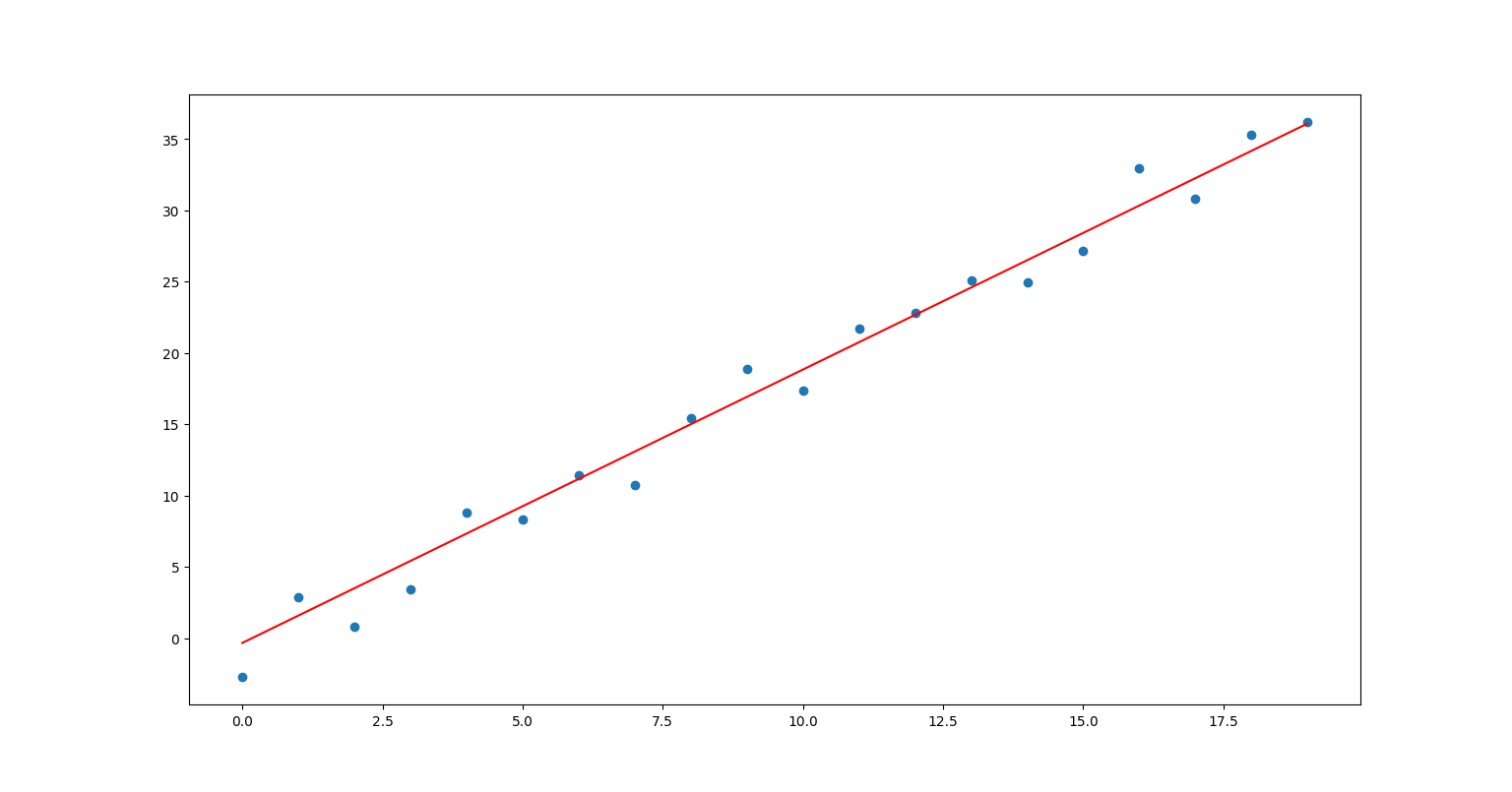
Figure_1

完整代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59


import numpy as np
import matplotlib.pyplot as plt

num = 20	# 散点数目

# --------------数据生成----------------
px = np.arange(num)
py = 2*px-4+5*np.random.random(num)	# 加上噪声

# 散点图
plt.scatter(px,py)
# plt.show()

# --------------模型搭建-----------------
# 模型函数
def f(x,k,b):
    return k*x+b

# 损失函数
def L(x,y,k,b):
    s = 0
    n = len(x)
    for i in range(len(x)):
        s += (k*x[i]+b-y[i])**2
    return s/2

# k梯度
def grad_k(x,y,k,b):
    s = 0
    n = len(x)
    for i in range(n):
        s += (k*x[i]+b-y[i])*x[i]
    return s/n

# b梯度
def grad_b(x,y,k,b):
    s = 0
    n = len(x)
    for i in range(n):
        s += (k*x[i]+b-y[i])
    return s/n

# --------------梯度下降-----------------
# 初始化参数
k = 0
b = 0

times = 100		# 训练次数
alpha = 0.01	# 步长

for i in range(times):
    # 梯度下降迭代
    k = k - alpha*grad_k(px,py,k,b)
    b = b - alpha*grad_b(px,py,k,b)
    if i%20 == 0:
        print("%d:%.2f"%(i,L(px,py,k,b)))	# 输出当前损失函数

plt.plot(px,f(px,k,b),c = "red")	# 绘制训练结果
plt.show()